相位噪聲就是指石英晶體振蕩器在各種噪聲的作用下引起的系統輸出信號相位的隨機變化,描述無線電波的三要素是幅度,頻率,相位.頻率和相位相互影響.理想情況下,固定頻率的無線信號波動周期是固定的,正如飛機的正常航班一樣,起飛時間是固定的.頻域內的一個脈沖信號(頻譜寬度接近0)在時域內是一定頻率的正弦波.低相位噪聲是有源晶振中重要的一個性能.下面康比電子為廣大用戶簡述一下關于石英晶體振蕩的的噪聲及抖動.
噪聲和抖動簡介
頻率系統性能的測量是它的穩定性,即在合適的測量上頻率的波動水平.目標是將這些波動保持在最低限度;然而,噪聲和抖動在系統中是不可避免的,并且會對性能產生負面影響.
抖動:基本介紹
考慮一個有兩種狀態的信號,“開”或“關”.該信號在脈沖之間具有恒定的時間周期,并且所有脈沖的長度相等.
由于信號的性質,很容易預測下一個脈沖何時到達.如果你想建立一個利用這個脈沖特性的系統,你可以這樣做;例如,如果兩個脈沖之間的時間是幾秒鐘的倍數,你可以根據這個信號制作一個非常簡單的定時裝置.
然而在現實中,沒有什么事情是這么簡單的.再次考慮這個信號,但是現在也考慮一些破壞它的東西.這種“噪聲”,無論是來自脈沖內部還是外部參數,偶爾都會導致脈沖提前到達.
這本質上是抖動,可能會導致系統性能下降.
噪聲基礎
噪聲是來自內部或外部源的信號中的任何不想要的信息,一些是不可避免的,而另一些則可以從系統中移除.
內部噪聲(約翰遜-奈奎斯特噪聲)
有時稱為熱噪聲或白噪聲,是元件內電荷載流子熱運動的結果.噪聲水平取決于部件的電阻和溫度,并且在所有頻率下都是相同的,因此是不可降低的.約翰遜噪聲與帶寬成正比,其變化本質上是高斯的.這可以從功率譜密度得到.高斯意味著它均勻分布在中心點的兩側,中心點是平均值或平均值.它是一個鐘形曲線或正常曲線,如圖1所示.
圖1-示例高斯分布曲線
散粒噪聲
構成電流的電子的離散特性也在元件中引起噪聲.這在極低電流應用中變得非常重要.這也是白色的,不可約的.
閃爍噪聲
盡管Johnson和Shot噪聲獨立于電路和晶振元件設計,閃爍噪聲卻不是.閃爍噪聲(也稱為粉紅噪聲)在低頻占主導地位,是由于元件性能的瞬時波動.它遵循類似于功率=1/f的趨勢,其中f是頻率.因此,隨著頻率的增加,閃爍噪聲的功率趨于0.圖2.
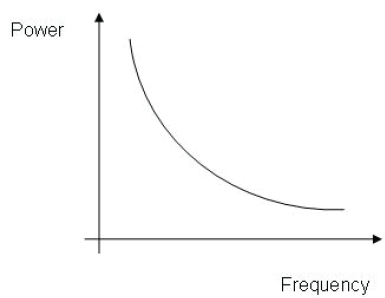
圖2
外噪聲
這是一種干擾.例子包括50Hz電源線路,電容和磁耦合.如果沒有適當的預先考慮,這可能會成為一個問題.
隨機游動
這是晶體結構本身固有的,包括沖擊和振動等環境源.這些很長
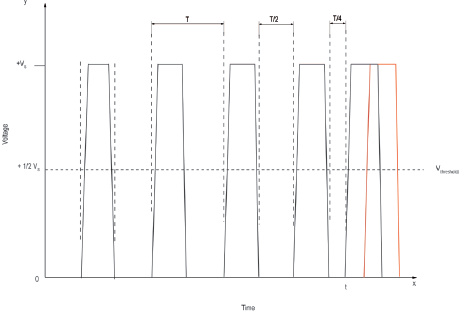
圖3
抖動和相位噪聲
影響晶體本身結構的術語因素可以被忽略.隨機游走通常被定義為小于10Hz,而不是抖動.
量化噪聲
通常表示為信噪比(SNR):以分貝為單位定義為SNR=20log10(Vs2/VN2)(1)其中Vs和VN分別是信號和噪聲的均方根電壓.
相位噪聲
對于這個討論,我們感興趣的是圍繞給定點振蕩的均勻周期波形.例如,在地(0V)和電源電壓(Vs)之間振蕩的方波.我們將考慮輸出通過Vs上升的點作為閾值參考有源晶振電壓,并使用該值測量脈沖的上升沿.我們不考慮上升沿0V的任何增加,因為這可能是隨機噪聲.或者,我們可以考慮一個關于水平x軸對稱的正弦波,其中x=0是我們的測量參考點,0V線.我們有效地尋找原始波形和接收波形之間的相位差,即信號的抖動.抖動用時間或單位間隔來描述,而相位噪聲用弧度或度數來描述.例如,考慮一個均勻的方波,它在0V和+Vs之間以1MHz的頻率振蕩,然而,感應到電路中的是噪聲,這意味著信號提前到達Vs.如圖3所示,最終波形比之前的波形更快地越過閾值電壓Vs;因為噪聲導致波形提前到達.在這種情況下,在0V下花費的時間是先前波形的一半.使用:T=1/f(2)
我們知道整個周期需要1秒.所以這個波形提前250秒到達.這是250納秒的抖動或π或90°的相移.可以通過數學分析來更清楚地描述相移和抖動的例子是正弦波形.正弦曲線可以用以下形式書寫:f(t)=Asin(ωt+θ)(3)其中A是波的最大振幅,ω=2πf,θ是相移.
例子:
考慮以下情況,x是頻率為1Hz的正弦曲線.波形方程為x=sin2πt.然而,噪聲存在,并導致波異相移動.圖4,5和6.
我們有一個0V的閾值電壓,當波穿過水平x軸時記錄時間.當時間穿過x軸時,測量值為0.4375秒.這是0.0625秒的抖動.由此我們可以計算出相移.從(3):f(t)=Asin(ωt+θ)f(t)=Asin(2πft+θ)f(t)=Asin(2πt+θ),f=1
f(t)=Asin(2πx0.4375+θ),因為波是0.4375s早期f(t)=Sin(2πx0.4375+θ),因為A=10=2πx0.4375+θ,在f(t)=00=0.875π+θ-θ=0.875πθ=0.125π
θ=1/8π相移
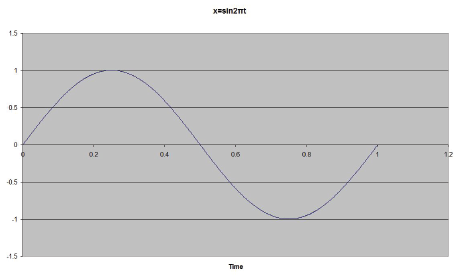
圖4-異相波形
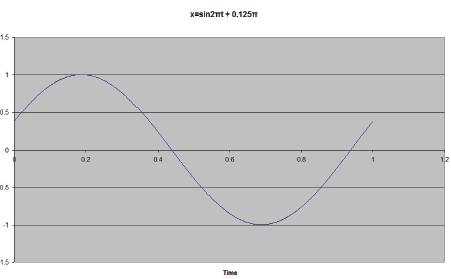
圖5-同一軸上的波形
圖6-粉色波形異相
相位噪聲圖
在前面的例子中,分析了單一的噪聲事件;然而,檢查信噪比(SNR)如何隨著頻率或噪聲的變化而變化也是有用的.這繪制在一個曲線圖上,在Y軸上顯示SNR值,在X軸上顯示距基頻的距離.頻率離基頻越遠,SNR將變得越小,如圖7所示.
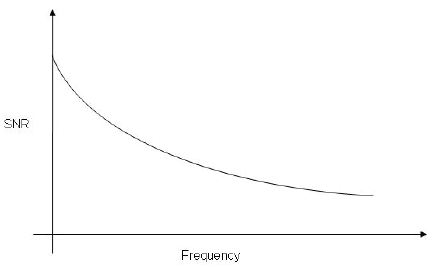
圖7
從圖表中,你可以找出不同的興趣點,例如,3dB頻率,SNR的功率減半.這使得能夠繪制顯示相位噪聲與偏移的圖表.
圖8中的圖表分解了石英晶體振蕩器所經歷的相位噪聲源.相位噪聲圖被分成五個主要區域,在水平X軸上與基頻有距離,在垂直Y軸上有SNR.你可以觀察到閃爍角,閃爍噪聲在信號中成為可忽略的因素;在這一點上,高于這個角頻率的所有噪聲變得不可減少.這與前面標注了噪聲區域的圖表非常相似.
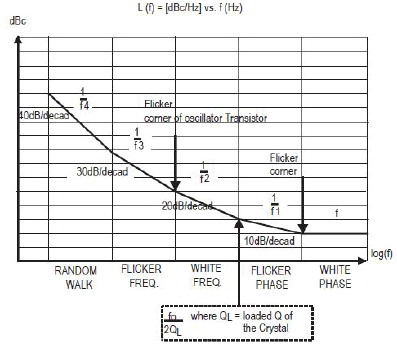
圖8-頻率噪聲圖
測量抖動
在介紹了抖動的基本概念之后,控制抖動的原則是合乎邏輯的和直接的;事實上,這是對理想波形和非理想波形之間差異的測量.然而,實際上進行測量可能相當復雜.在前面的例子中,我們將測量信號與理論上的理想信號進行了比較.然而,在現實世界中,沒有信號是完美的,要進行測量,你必須有一個干凈的信號來比較,即一個噪聲非常小的信號.
周期和周期間抖動
周期抖動是時鐘周期應該處于的位置和它看起來所處的點之間的差值.這是理想脈沖應該到達的時間和脈沖實際到達的時間之間的時間差.
周期間抖動是兩個連續時鐘周期之間的差值,由此引入系統的抖動導致下一個理想信號的變化.
例如,考慮一個在地和+Vs之間振蕩的均勻波形,其標稱周期為T.然而,抖動會導致波形在某個時間到達.我們可以說周期到周期抖動是T-t.周期到周期抖動很難測量,因為理想波形的周期是基于前一個波形的周期.為了找到下一個周期到周期的抖動,我們將下一個周期的周期與前一個周期進行比較.這通常需要使用能夠測量比波形頻率更快的信號的高速定時設備.
一種方法是將長期標稱頻率的平均值作為參考.假設噪聲是隨機的,并且具有高斯分布曲線,其平均值為0.由此可見,平均頻率不會與理論標稱頻率不同.然后在短時間內測量這個平均值的微小變化,給你信號的抖動.然而,當你考慮取暖,改變環境因素和隨意走動時,這可能會導致問題.另一種方法是使用參考信號,一種與感興趣的成分具有相同標稱頻率的干凈源.貼片晶振需要具有可控頻率.我們需要用合適的反饋系統消除所有外部干擾.我們也需要創建一個反饋回路來保持它們的平均長期頻率相同,這被稱為鎖相.你將可控源“鎖定”在感興趣的成分上,比較它們的長期平均頻率.這消除了隨機行走的問題,因為它允許測量信號行走,而可控源由于反饋回路而“行走”等量.即使組件被鎖定在一個循環中,它仍然會抖動.出于測量目的,我們對信號何時超過閾值電壓感興趣.(我們定義的興趣點;在前面的例子中,給出了X軸上Vs的1/2.))
我們感興趣的是抖動在兩個分量的閾值電壓中造成時間差的點.這兩次的差異將向我們展示組件的抖動.根據這些值,我們可以繪制記錄值的直方圖.
均方根抖動(σ)
根據所示示例,記錄的數據以高斯分布曲線呈現,也就是說,它遵循正態分布模式.抖動的隨機來源通常就是這種情況.
從這些數據的高斯分布可以得出一個有趣的觀察結果.我們可以通過它的寬度來確定均方根抖動σ.此外,我們還可以觀察到平均抖動為0,這僅是理想高斯分布的情況.
峰間抖動
描述測量的抖動的另一種方式是通過取均方根值的合理大倍數來顯示峰值.常見選擇是使用14σ的峰峰值(pk-pk)值.任何超出此范圍的值都將非常罕見,幾乎可以忽略不計.如果系統在兩點之間有界,那么最壞的情況就是系統有界邊緣之間的峰值.然而,請注意,這是假設有界邊不允許輸出電平在定義的邊之上或之下有任何波動.圖9.
圖9
對于不適合高斯或有界場景的系統,我們使用類似于高斯系統的程序.我們取樣本的平均值,從這一點開始,移動足夠遠,以至于這些點的抖動很少,可以忽略不計.
抖動的頻率分析
另一種顯示抖動的方法是通常通過使用頻譜分析儀在頻域中進行測量.再一次,我們比較了如上所述的清潔無噪聲源,兩者都被鎖相以允許行走.在一個理想的世界里,我們會在顯示器上看到一個峰值響應,但是實際上它會顯示一個清晰的信號,兩邊都有裙子;這些裙部是破壞信號的抖動的產物.通常由于粉紅色噪聲,信號的兩側可能會出現低幅度尖峰或雜散.
圖10.請注意,當波形變寬并遠離主頻率時,主信號和裙邊的定義尖峰.
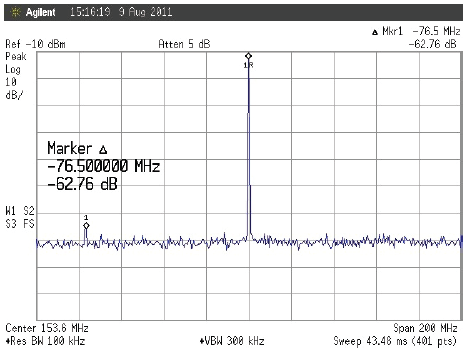
圖10-抖動的示例頻譜分析圖
量化抖動
上面我們展示了如何通過使用信噪比來量化噪聲,而對于抖動,我們通常將其表示為預期脈沖和實際到達的脈沖之間的時間差.對于在兆赫范圍內工作的系統,通常以皮秒為單位量化抖動測量值.
振蕩器中的抖動
如果振蕩器設計正確,并且輸出頻率與壓電石英晶振的固有諧振頻率相匹配,則振蕩器中的抖動應該僅來自隨機源.振蕩器中的隨機抖動應該足夠小,以皮秒為單位進行測量.所有振蕩器都應該是這種情況,即使對于那些其輸出是從晶體振蕩器的正弦波輸出導出的方波信號的振蕩器也是如此.
由于可編程晶體振蕩器輸出頻率的產生方式,其抖動通常較大.他們通常使用鎖相環(PLL)的頻率生成方法,這可以增加他們對抖動的敏感度,通常在100psrms的數量級.考慮可能從外部系統引入系統的抖動是有用的.如果低抖動信號對于系統的工作是必不可少的,那么選擇具有低抖動值的組件是不夠的,應該決定設計一種將抖動最小化的電路.例如,屏蔽部件和電路免受干擾可能就足夠了,或者在電源線中放置簡單的RC濾波器可以幫助衰減來自電源的所有高壓紋波.振蕩器的輸出信號可能是純凈的,但是它所在的電路很容易受到噪聲和抖動的影響.
抖動效應
由于大多數數字系統依賴通用時鐘總線,我們關心的是一個電路是否能容忍時鐘脈沖定時的任何微小變化.
在數字通信系統中,編碼數據通常被長距離發送,然后一旦接收就被解碼.然而,需要有一個公共時鐘來允許脈沖被解碼,并且如果其中任何一個的時鐘受到抖動的影響,則可能會有來自源的數據完整性的一些損失.同樣,在選擇合適的石英晶振之前,值得考慮你的應用.